Philosophy & Objectives
Reseach Philosophy
In the design of a reinforced concrete structure, governing standards typically require that the structural components be proportioned according to the results of linear elastic analyses of force distribution. The design thus achieved normally meets strength and serviceability criteria, albeit perhaps not most efficiently. During the life of the structure, however, situations may arise where a more accurate assessment of the structure's strength and expected behaviour is required. This is particularly true in instances where the structure requires repair, rehabilitation or requalification to newer and more stringent code requirements; an increasingly common occurrence now that we are in an era where expenditures on rehabilitation outweigh those spent on new construction. Concerns may relate to cracking and deformation under service loads, safety and functionality under extreme or accident loads, ultimate load capacity, ductility and energy dissipation capacity or collapse mechanisms. To address such concerns, advanced nonlinear methods of analysis must be employed. Thus, there is a growing need for analysis tools that accurately model the performance of concrete structures.
In developing advanced analysis procedures, the common approach has been to first formulate a sophisticated nonlinear algorithm, and then to implant some rudimentary model for concrete. There are two inherent weaknesses in this. First, the concrete modelling is usually based on classical mechanics formulations that typically fail to capture the influence of various important second-order mechanisms. Secondly, the analysis algorithms employed are usually generic, not specifically formulated for reinforced concrete, and typically have difficulty in responding to the dramatic changes in stiffness and behaviour associated with cracked concrete structures. Consequently, traditional approaches to nonlinear performance modelling have met with only limited success, as seen in the results of several international prediction competitions. The large commercially available software packages are typically of little use in this regard.
At the University of Toronto, the favoured approach to formulation of advanced analysis procedures is one that places heavy emphasis on accurately describing the constitutive response of cracked reinforced concrete. A six-faceted methodology, as illustrated, can be described as follows:
(i) Formulate a simple and rational theoretical model for the mechanism or behaviour being studied.
(ii) Develop a reliable data base through experimental investigation, emphasizing well-defined conditions on simple elements.
(iii) Formulate, from the test data, simple but realistic constitutive models that accurately reflect response under states and conditions of practical concern.
(iv) Implement the theory and models into numerically robust nonlinear analysis algorithms specially formulated for reinforced concrete.
(v) Verify the analytical procedures against tests involving more complex structures.
(vi) Apply the analysis procedures to real situations, sometimes exposing weaknesses in the formulations where additional work is required. In this manner, analysis tools that are of practical value can be developed.
Research Objectives
The research completed to-date represents a tightly focussed effort towards developing advanced nonlinear procedures for analysis of reinforced concrete structures. Going forward, the envisaged research will build on this foundation. The primary aim will be to develop computer-based performance simulation models that can be used in practical situations to provide accurate predictions of the behaviour of concrete structures under normal and extreme conditions. Emphasis will be placed on developing design office friendly tools that are applicable to the practical problems being faced by designers today, enabling assessments of the strength, safety and performance capability of structures in their current state, and under postulated repair or rehabilitation schemes. Particular attention will be paid to performance modelling, and to proper consideration of rehabilitation chronology. A prime area of focus will be on the behaviour of structures subjected to extreme loads including blast, impact and high temperature.
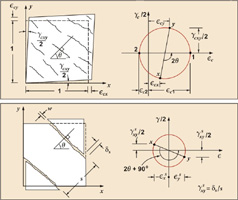
Step 1: Theory
Formulate rational theory for RC behaviour (Compatibility conditions for disturbed stress field model shown)

Step 2: Experimental investigation
Obtain data from simple tests (Panel element shown)
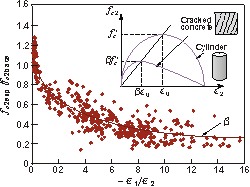
Step 3: Constitutive modelling
Formulate realistic behaviour models from test data (Compression softening model shown)
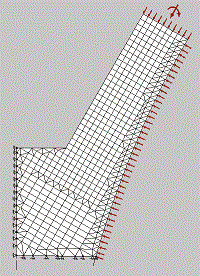
Step 4: Implementation
Implement into analysis procedure (Model for FEA program VecTor2)

Step 5: Verification
Verify models and analysis procedures with large-scale tests (Plane frame specimen being tested)
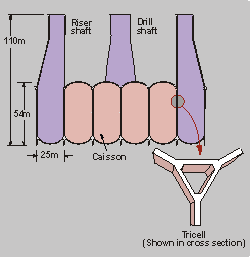
Step 6: Application
Apply to practical problems (Analysis of Sleipner A details)